Visually Guided Robots | Visual Tracking | 3D Models from Images | Segmentation and Grouping

Curves and Surfaces

The reconstruction of surfaces from apparent contours
In this project we aim to recover the shape of arbitrary surfaces from the apparent contours (or outlines) visible from arbitrary views. A key contribution is the introduction of the epipolar parametrization which exploits the epipolar geometry (geometry of viewpoints) to induce a spatio-temporal parametrization of the image curves and surfaces. This generalizes the epipolar geometry of points to curves and surfaces, and allows the recovery of shape under perspective projection and arbitrary camera motion.
Further Information

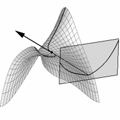The analysis of the degeneracies of the epipolar parametrization

Singular apparent contours or cusps occur at isolated points, seen as an abrupt contour ending in the outline of an opaque surface. The epipolar parametrization cannot be used to recover surface geometry at these points. In this project, the locus of cusps under viewer motion is exploited to recover the geometry in the vicinity of the cusps. The other case of degeneracy is used to develop an algorithm to recover viewer motion.

Recovery of camera motion from outlines
It is generally believed that the outlines of a curved surface cannot be used to recover the motion since they are projections of curves which slip over the surface under viewer motion. In this project, the envelope of consecutive contour generators is shown to define special (frontier) points and these points are used to recover the epipolar geometry from image curves.

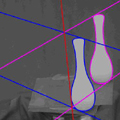Circular motion

In this project, a particularly simple and elegant solution is found for a special type of motion in which an object is placed on a turntable which is rotated in front of a stationary camera. A novel solution is introduced which exploits the symmetry in the envelope of outlines swept out by the rotating surface. This technique uses a single curve tracked over the image sequence and has been successfully used to recover the shape of an arbitrary object from an uncalibrated camera.
Further Information

Quasi-invariant parametrizations and matching of curves

In this project we aim to develop a robust algorithm for curves mathcing. B-splines can be fitted automatically to image edge data and used to group fragments of curves which are projections of bilateral symmetry in the scene. Quasi-invariant parametrizations of image curves are developed to help in the matching of curves. These reduce the order of derivatives required to compute the geometric invariants of curves from fifth to second-order making these less sensitive to image noise and occlusion.
Further Information

Visually Guided Robots | Visual Tracking | 3D Models from Images | Segmentation and Grouping

Return to Research Pages